How Do You Know the Constant of Proportionality

marzo 13, 2022 Publicar un comentario

Constant of Proportionality

When two variables are straight or indirectly proportional to each other, then their human relationship can exist described equally y = kx or y = k/x, where k determines how the two variables are related to ane another. This k is known as the constant of proportionality.

1.	What is Constant of Proportionality?
two.	Why Practice We Use The Constant of Proportionality?
3.	How to Solve The Constant of Proportionality?
iv.	Identifying The Abiding of Proportionality
five.	Solved Examples
vi.	Practice Questions
7.	FAQs on The Constant of Proportionality

What is Constant of Proportionality?

Constant of proportionality is the constant value of the ratio betwixt two proportional quantities. Two varying quantities are said to exist in a relation of proportionality when, either their ratio or their product yields a constant. The value of the constant of proportionality depends on the blazon of proportion betwixt the 2 given quantities: Direct Variation and Inverse Variation.

Direct Variation: The equation for direct proportionality is y = kx, which shows as x increases, y as well increases at the aforementioned rate. Example: The toll per particular(y) is directly proportional to the number of items(10) purchased, expressed equally y ∝ x
Inverse Variation: The equation for the indirect proportionality is y = k/x, which shows that as y increases, x decreases and vice-versa. Example:The speed of a moving vehicle (y) inversely varies as the fourth dimension taken (x) to embrace a certain distance, expressed equally y ∝ 1/ten

In both the cases, k is constant. The value of this constant is called the coefficient of proportionality. The constant of proportionality is besides known as unit charge per unit.

constant of proportionality in direct and inverse variation

Why Do Nosotros Apply The Constant of Proportionality?

Nosotros apply abiding of proportionality in mathematics to calculate the charge per unit of change and at the aforementioned time make up one's mind if it is direct variation or inverse variation that nosotros are dealing with. Let us assume that the cost of 2 apples = $20. We determine that the toll of 1 apple tree = $x. Nosotros have constitute the Constant of Proportionality for the cost of an apple is 2.

If nosotros want to draw a picture of the Taj Mahal past sitting in front of it on a piece of newspaper by looking at the real image in forepart of united states of america, nosotros should maintain a proportional relationship between the measures of length, height, and width of the building. Nosotros need to place the constant of proportionality to get the desired issue. Based on this, nosotros can depict the monument with proportional measurements. For instance, if the height of the dome is ii meters and then in our drawing we can represent the aforementioned dome with height 2 inches. Similarly, we can depict other parts. In such scenarios, nosotros use abiding of proportionality.

Working with proportional relationships allows one to solve many real-life problems such every bit:

Adjusting a recipe's ratio of ingredients
Quantifying take chances similar finding odds and probability of events
Scaling a diagram for drafting and architectural uses
Finding percent increment or percent decrease for price mark-ups
Discounts on products based on unit rate

How to Solve The Constant of Proportionality?

We apply our knowledge on the direct and inverse variations, identify them and then determine the abiding of proportionality and thereby get the solutions to our problems.

Example 1:Detect the abiding of proportionality, if y=24 and ten=three and y ∝ x.

Solution: We know that y varies proportionally with x. We tin write the equation of the proportional human relationship every bit y = kx. Substitute the given x and y values, and solve for k.

24 = k (3)

k = 24 ÷ 3 = 8

Therefore, the abiding of proportionality is 8.

Case two: four workers take 3 hours to finish the desired work. If ii more than workers are hired, in how much time will they complete the piece of work?

Solution: Let x1 = number of workers in case 1 = 4

x2 = Number of workers in example 2 = 6

y1 = number of hours in example one = 3

y2 = number of hours in case 2 = To be found

If the number of workers is increased, the time taken to complete will reduce. We find that number of workers is inversely proportional to the time taken, (y1 = k/x1) ⇒ 3 = 1000 / 4⇒ k = 12

Again, to find the number of hours, (y2 = chiliad/x2) ⇒ y2 = 12/vi= 2 hours.

Identifying The Constant of Proportionality

We shall now learn how to place the constant of proportionality (unit of measurement rate) in tables or graphs. Examine the tabular array below and make up one's mind if the human relationship is proportional and detect the abiding of proportionality.

Number of Days = ten	1	iii	5	6
Number of Manufactures Written = y	3	ix	15	18

We infer that equally the number of days increases, the ariticles written also increases. Hither we identify that it is in directly proportion. We apply the equation y= kx. To find the constant of proportionality nosotros determine the ratio between the number of articles and the number of days. Nosotros need to evaluate for k = y/x

y/ten = 3/ane = nine/3 = 15/five = 18/half dozen = 3

From the result of the ratios of y and 10 for the given values, nosotros can observe that the same value is obtained for all the instances. TheConstant of Proportionality is iii.

If nosotros plot the values from the above table onto a graph, nosotros find that the directly line that passes through the origin shows a proportional relationship. The constant of proportionality under the direct proportion condition is the slope of the line when plotted for two proportional constants x and y on a graph.

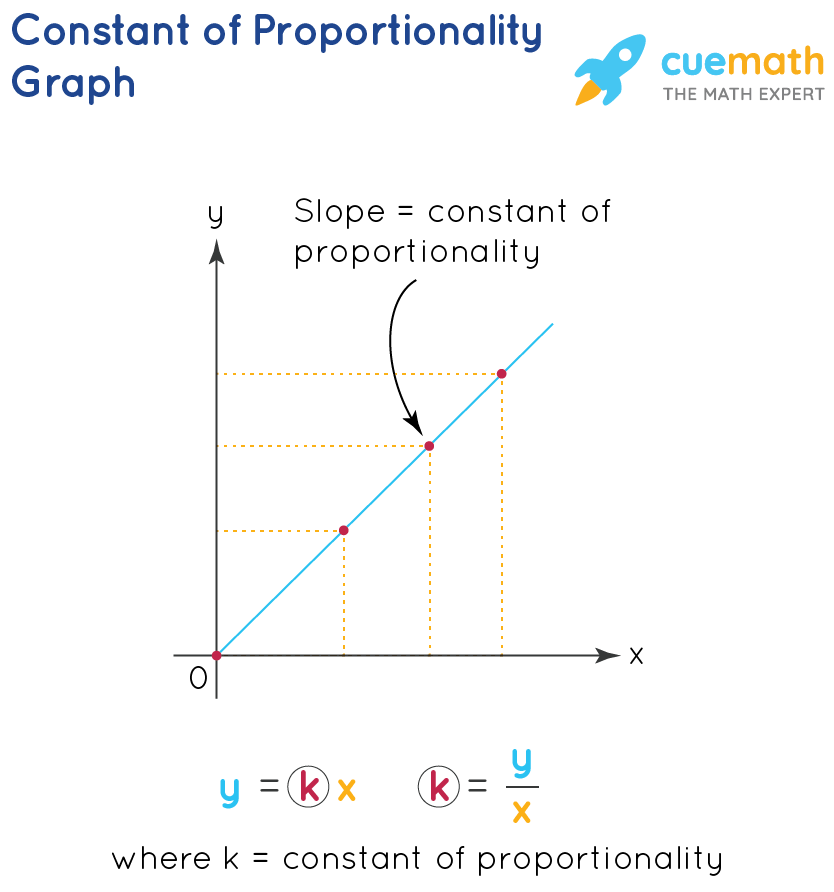
constant of proportionality in direct and inverse variation

Related topics to Constant Of Proportionality

Changed Proportion Formula
Straight Proportion Formula
Abiding of proportionality Calculator

Important notes

To check if the 2 quantities are proportional or not, we have to find the ratio of the 2 quantities for all the given values. If their ratios are equal, and so they exhibit a proportional relationship. If all the ratios are not equal, then the relation betwixt them is non proportional.
If two quantities are proportional to 1 another, the relationship between them can exist defined byy = kx, where k is the constant ratio of y-values to corresponding x-values.
The same relationship can also be defined by the formula 10=(1/k)y, where one/one thousand is now the constant ratio of ten-values to y-values.

Example 1: Look at the tabular array beneath. Practise the variables showroom whatever blazon of proportion? If so, what is the constant of proportionality?

X	Y
5	1
25	5
16	3
35	7

Solution:

To check the constant of proportionality, nosotros use: y = kx

chiliad = y/x

y/10 = 1/5 = five/25 =seven/three ≠ three/16

Nosotros tin find that all the ratios in the higher up table are not equal. Hence, these values are NOT in a proportional human relationship.

Instance 2: Let us assume that y varies directly with x, and y=30 when 10=6. Use the constant of proportionality and observe the value of y when x=100.

Solution: Firstly, we should write the equation of the constant of proportionality, y = kx. Substitute the given x and y values, and solve for k. 30 = k × six ⇒ 1000=5

The equation is: y = 5x. Now, substitute ten=100 and notice y

y= 5 × 100 = 500
Therefore, the value of y is 500 when x=100.
Example 3: Anthony takes 15 days to reduce 30 kilograms of his weight by doing xxx minutes of exercise per day. If he exercises for i 60 minutes and 30 minutes every mean solar day, how many days will he accept to reduce the same weight?

Solution:

According to the situation, weight and exercise are inversely proportional. As the number of minutes of workout increases, Anthony's weight reduces. Let m be minutes and d be days.
grand =k/d. Allow us accept m1 = 30, m2= 90, d1 = 15. We are required to find d2.

m1 = k/d1
k = 30 × 15 = 450 (Substituting the known values, determine k)

m2 = m/d2

90 = 450/d2

d2 = 450/90 = 5(Substituting the known values, determine d2)

Therefore, if Anthony exercises for 1 hour and 30 minutes per day, information technology volition take only 5 days to reduce 30 kilograms of weight.

become to slidego to slidego to slide

How can your kid main math concepts?

Math mastery comes with practise and understanding the 'Why' behind the 'What.' Experience the Cuemath difference.

Book a Free Trial Grade

FAQs on Constant of Proportionality

What is the Other Name for the Abiding of Proportionality?

Another name for the constant of proportionality in mathematics is the unit rate.

What is the Constant of Proportionality in a Graph?

The straight line that passes through the origin is the constant of proportionality in a graph.

Why exercise we Utilise Constant of Proportionality?

We employ constant of proportionality in mathematics to determine the nature of proportionality, whether it is directly proportion or indirect proportion. The abiding of proportionality helps in solving the equations involving ratios and proportions.

What is the Constant of Proportionality of 12/six?

To detect the constant of proportionality, in the case of directly proportionality, we apply thousand=y/x. Permit us accept y = 12 and 10 = 6, then k = 12/6 = 2.

What is the Constant of Proportionality?

If the ratio of ane variable to the other is constant, then the ii variables have a proportional relationship, If x and y have a proportional human relationship, the constant of proportionality is the ratio of y to x. Sometimes, we likewise represent it every bit x is to y.

sheffieldobtlyn.blogspot.com

Source: https://www.cuemath.com/commercial-math/constant-of-proportionality/